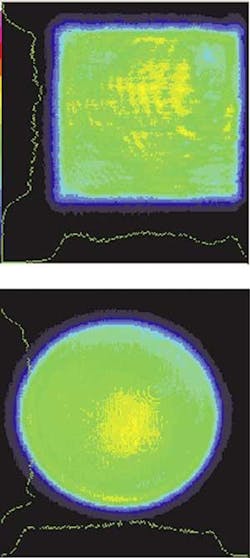
Rarely can a useful task be performed with only the raw beam energy emerging from a laser. Shaping the laser beam—even if nothing more than focusing the beam with a lens—is critical to almost every laser application. Many techniques can be used to shape the intensity and phase profile of a laser beam.1 Shaping a Gaussian laser beam into a uniform round or square beam is just one application (see Fig. 1).
null
Highly efficient laser-beam shaping of standard laser sources can be accomplished with diffractive, refractive, or reflective elements. Each of these techniques has certain advantages and limitations. Laser sources from carbon dioxide at 10.6 µm to excimer at 193 nm can be usefully shaped, but some techniques work better at certain wavelengths than at others. The transverse mode structure and stability of a laser, single or multimode, is also important in choosing a particular beam-shaping technique. Complex shapes can be realized by choosing the right beam-shaping technique to match the application and specific laser.
Why shape a beam?
Shortly after the first lasers were operating in laboratories in the early 1960s, scientists began developing ways to efficiently shape Gaussian laser beams into uniform intensity profiles. In the early 1990s, these beam-shaping techniques began making their way into commercial laser systems. The fundamental TEM00 mode is a round beam with a Gaussian intensity profile; this shape is suitable for many precision laser applications. However, a uniform or "tophat" profile is often more desirable for certain applications. Such applications include photolithography, material processing, cutting and drilling, entertainment, alignment, targeting, and many others.
The tophat profile can either enhance system performance or provide source properties that are essential to the application. Multibeam lithography, used for fabricating submicron grating structures, requires stable laser beams with flat phase and intensity profiles. Optical computing applications also generally require similar uniform beam profiles. In the past, system designers often produced such profiles by expanding the beam and using only the central, approximately flat, portion of the beam. Although simple and inexpensive, this obviously wastes much of the available energy in the laser beam.
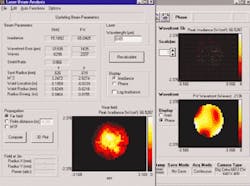
Materials processing and hole drilling with lasers can be enhanced with properly shaped beams. Many users want the laser energy distributed uniformly over a round, square, or rectangular area. Holes drilled in printed-circuit boards with a frequency tripled Nd:YAG laser at 355 nm, for example, can be drilled faster and more cleanly and sharply with proper beam shaping (see Fig. 2). Uniform profiles as small as 22 µm are being efficiently formed with 355-nm-emitting lasers using beam shaping. Carbon dioxide lasers emitting at 9.3- to 10.6-µm are incorporating beam shaping to drill holes as small as 100 µm. Profitability improves with increasing efficiency and speed of fabrication.
null
Entertainment and alignment/targeting applications typically require lasers to produce complex geometric shapes. Companies have transformed the red dot of laser pen pointers into arrows, dollar signs, company logos, and even the faces of company executives. Crosshairs, letters, and other shapes have been used with infrared laser diodes for military targeting applications. Diffractive diffusers and beam shapers have been used in optical printer heads and optical data storage devices.
Techniques used in beam shaping
Beam shaping can be divided into two basic categories. The first category, often called beam transformers, performs a one-to-one mapping of points in an input plane to points in an output plane. The simplest example in this category is a Gaussian-to-tophat shaper for a single-mode laser. The second category includes band-limited diffusers, diffractive beamsplitters, and beam integrators. This category of beam shapers performs a many-to-one mapping of points in one plane to multiple points in another plane of the beam. The beam is broken up into multiple beamlets and either overlapped (beam integration) or directed into different directions (diffusers and beamsplitters).
The beam transformer can only be used with a high-quality, near TEM00 Gaussian laser beam. Diffractive, refractive, or reflective elements can be used to transform the intensity and phase profile of the beam into some other desired shape. If only the intensity needs to be shaped at a single target plane, then only one shaper element is necessary. If wavefront phase must also be corrected (for example, collimated or redirected into a spherical wavefront), then at least two shaper elements separated by a distance are necessary. The advantages of beam transformers are that the output laser beam can be recollimated, focused, or expanded, and the pattern contains no speckle. If the input beam is stable with a low M2 factor, the output beam can achieve a very uniform, steep-sidewall intensity profile. Shortcomings of the transformer approach include extreme sensitivity to input beam parameters and very tight optical-alignment tolerances. Transformer designs degrade if the input beam is unstable or varies considerably from the expected input beam profile.
Another example of beam transformation is circularizing the output of laser diodes. Efficient coupling of laser-diode energy into a single-mode fiber requires matching the numerical aperture (NA) of the focused light to that of the fiber, which requires a circular output from the laser. The typical elliptical beam shape of a laser diode does not readily lend itself to NA-matching to the circular core of the fiber. A two-sided anamorphic refractive microlens, fabricated in gallium phosphide, was recently fabricated and tested at MEMS Optical for circularizing laser diodes (see Fig. 3).
null
Beam integrators are used to smooth out intensity-profile fluctuations in the beams of high-power multimode lasers. A microlens array—which can be diffractive, refractive, or reflective—breaks the beam up into multiple smaller beamlets. The beamlets are then overlapped at a target plane with an integrator lens. The overlapping produces interference effects, but these are usually mitigated by the time-dependent intensity fluctuations. Another shortcoming of the integrator approach is that the beam cannot be recollimated. The uniform intensity pattern is produced at a single target plane.
Diffractive beamsplitters and diffusers break up the beam into either a finite number or near continuum of multiple diffraction orders. The fraction of beam energy directed into each order is designed into the element to produce the desired complex pattern. The complexity of these patterns can range from simple geometric shapes and arrays of dots to very complex images of human faces.
How shaped beams propagate
A low-M2 Gaussian laser beam maintains its Gaussian shape over a large propagation distance. This is not true, in general, of shaped profiles. Just as a hard aperture inserted in a laser beam causes diffractive ringing in the profile after only a short propagation distance, so a sharp tophat will quickly degrade with propagation distance. Rounding the corners of the tophat into a high-order super-Gaussian that approximates the desired tophat shape can reduce these diffraction effects.
Physical-optics propagation software can be used to model the diffraction effects as the beam propagates. If the profile does not sufficiently maintain its shape over the desired propagation distance, shaping to a lower-order super-Gaussian can be tried. Alternatively, a lens can be used to re-image the tophat to a different location in the beam path.
Free-space propagation of high-power beams in the atmosphere suffers from thermal blooming effects. Contrary to what one might expect about Gaussian vs. non-Gaussian beam propagation, experimenters have found that beam shaping mitigates the thermal blooming effects and allows propagation over longer distances.2
Designing beam shapers
Simple beam transformers and beam integrators can be designed with most ray-tracing lens-design codes, as long as one can easily redefine the merit function. Ray targets are generated by determining the integral of the beam energy as a function of radial position for both the input and output planes. For a Gaussian-to-tophat transformer, an analytic expression can be derived. For a Gaussian-to-super-Gaussian, the integration must be done numerically.
For rotationally symmetric on-axis beam transformers, ray targets need only to be generated along one radial line in the pupil. Axially symmetric transformers using diffractive optical elements often have the problem of the zero-order light interfering with the shaped light, particularly with the shorter wavelengths. This produces undesirable interference rings in the output. This problem can be eliminated with more-complex off-axis designs in which the zero-order light becomes spatially separated from the shaped pattern at the output. In such a system, the symmetry is reduced to being bilateral and ray targets must be defined in a full one-half of the pupil.
Designing complex diffusers, beamsplitters, and complex transformer shapes generally cannot be accomplished with ray-tracing codes. Some sort of iterative forward-backward propagation technique, such as the Gerchberg-Saxon algorithm, must be used. The desired pattern is scanned into the computer and the program gradually homes in on a solution.
Increasing complexity
Laser-beam shaping is becoming commonplace in commercial applications as systems engineers increasingly become aware of what it can accomplish. These beam-shaping schemes can be used across the wavelength range of current laser systems. Both integrating and transforming beam-shaping approaches have their pros and cons. Considering these pros and cons and deciding which approach is best for the particular application is critical to achieving a successful product. These shaped beams can be delivered to a working plane in many varied shapes and sizes, depending on the need for a given application. Current development work in beam shaping is concentrated on improving uniformity, conversion efficiency, and making more-complex shapes.
REFERENCES
- F. M. Dickey, S. C. Holswade, Laser Beam Shaping, Theory and Techniques, Marcel Dekker (2000).
- R. K. Tyson, Principles of Adaptive Optics, Academic Press (1991).
DANIEL M. BROWN is optical design manager at MEMS Optical, 205 Import Circle, Huntsville, AL 35806; e-mail: [email protected]. KURT KANZLER is president of Diffractive Laser Solutions., 949 Santa Ynez Way, Sacramento, CA 95816; e-mail: [email protected].