INTERFEROMETERS: Radial-polarization interferometer tops Michelson capabilities

Researchers at the Hebrew University of Jerusalem have developed a new radial-polarization interferometer (RPI) that is able to measure smaller phase changes than a conventional Michelson interferometer.¹ By combining the concepts of spatially inhomogeneous polarization fields (other than circular, elliptical, or linear) with orthogonal-polarization interferometry (using orthogonally polarized beams in the interferometry setup), the RPI instrument generates a spatially varying intensity pattern along the beam unlike standard Michelson interferometry—a pattern that yields additional spatial and phase information that can improve displacement and phase-change measurements.

A bit more complex

The RPI test setup is a modified version of the conventional Michelson interferometer. A laser beam linearly polarized in the x direction passes through a half-wave plate that rotates the polarization 45° from the x axis. A polarizing beamsplitter then divides this beam into two linearly and orthogonally polarized beams. Each of these beams then passes through a quarter-wave plate oriented at 45° from each beam's polarization axis and bounces back from a mirror (with one mirror on a translation stage) toward the quarter-wave plate and the polarizing beamsplitter. In effect, two spatially overlapping beams that are linearly and orthogonally polarized with respect to each other are generated.

The beams then pass through a space-variant subwavelength grating (developed by the researchers) to convert the orthogonal, linear polarizations into radially and azimuthally polarized beams. Finally, the beams pass through a linear polarizer serving as an analyzer and the plane of the analyzer is imaged to a CCD camera.

The need for a CCD camera makes the experimental setup of the RPI a bit more complicated than a Michelson interferometry setup, which only requires a single detector. To measure displacements using an interferometer, translation of the mirror modifies the phase difference between the two arms of the interferometer, causing an intensity change on the detector (typically a digitized detector with a finite number of bits). Neglecting all error sources except quantization error, the detection resolution of phase changes is limited by the least significant bit of the detector.

In contrast, with the RPI the intensity distribution on the camera for a given phase difference is not uniform. Instead, it is spatially varying across all pixels of the camera, and phase changes below the least significant bit of a detector can be recorded. In calculations, the minimum detectable phase change of the RPI (using an 8 bit, 1024 × 1024 pixel camera) was always found to be three to four orders of magnitude smaller than for the Michelson interferometer, meaning the RPI is capable of measuring much smaller displacements.

Additional capabilities

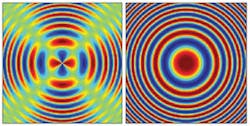
Besides measuring displacement, the RPI also improves over the Michelson approach for retrieving the phase profile of a test object placed in one arm of the interferometer. In a side-by-side comparison of RPI and Michelson with a test object consisting of a lens with a circular symmetric quadratic phase profile, two very different interferograms are captured by a CCD (see figure). Even though both have the same number of fringes, the RPI interferogram shows an intensity minimum every π phase shift along the radial coordinate, while the Michelson interferogram shows minimum intensity every 2π along the radial coordinate. This difference means that RPI is better suited to capture the phase profile of the test object, since detection of a small intensity change in a shot-noise-limited system is more accurate in the vicinity of a minimum (there are twice as many in the RPI interferogram) due to the lower noise level.

"Numerical simulations and experimental results show the feasibility of the proposed approach for achieving higher accuracy in phase change measurements," says Gilad Lerman, a PhD candidate at The Hebrew University of Jerusalem. "The approach may also provide better characterization of test objects," adds Uriel Levy, a faculty member at the Hebrew University. "Yet, additional experimental effort and improvement of the data-acquisition algorithm is required in order to take full advantage of the proposed approach."

REFERENCE

1. G.M. Lerman and U. Levy, Optics Express 17(25), p. 23234 (Dec. 7, 2009).