Spectroscopy: High-resolution spectrometers shrink down with SWIFTS

CHRISTOPHE BONNEVILLE

Optical spectrometers are used in a variety of applications-including those in major global fields such as medical diagnostics, industrial process monitoring, energy, and security—and have the potential to be used in many more. However, this potential will depend on the competitiveness of the spectroscopic solutions available on the market in terms of performance, cost, and integration capability.

We are still some way off from offering solutions that place spectroscopy on an equal footing with temperature sensors, image sensors, or gyroscopes, especially if we consider that a considerable proportion of the emerging applications in question can only be addressed by what is generally described as "high-resolution" spectroscopy—that is to say, having a resolution of better than 0.1 nm.

Indeed, both grating and Fourier-transform spectrometers (FTS) face difficult trade-offs between resolution, measured wavelength range, speed, size, and long-term robustness of the calibration. In contrast, the stationary-wave integrated Fourier-transform spectrometer (SWIFTS) is a new type of spectroscopic instrument that is not subject to such trade-offs and thus can solve this market-fit issue.

Probing an optical standing wave

In 1886, Gabriel Lippmann, a Franco-Luxembourgish physicist, turned his research to a method of fixing the colors of the solar spectrum on a photographic plate. Lippmann's idea was to image a scene on a mirror and to record the standing waves generated in the thin volume next to the mirror by the light reflected back upon itself. He succeeded in creating impressive color photographs by projecting the image onto a plate coated with a thin and nearly transparent photographic emulsion containing submicroscopically small silver halide grains and a temporary mirror on the top. For the color photograph to be viewed, the revealed plate had to be illuminated by white light.

The Lippmann process was at that time not easy to use in practice. But in 2004, two French researchers, Etienne Le Coarer from Joseph Fourier Grenoble University (Saint-Martin-d'Hères, France) and Pierre Benech from INP Grenoble (Grenoble, France), decided to bring Lippmann's ideas up to date by coupling sensing elements to the evanescent part of standing waves created within a single-mode waveguide. This led to SWIFTS, a "detector" capable of identifying the Fourier transform of a wave's spectrum over a wide range of wavelengths without using any moving parts, all within a minimal space.

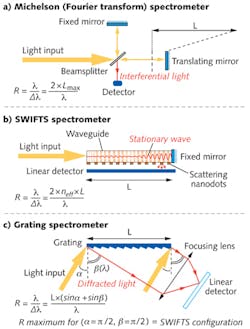
In SWIFTS, the standing wave is created in a single-mode waveguide ended by a fixed mirror (see Fig. 1). The evanescent-field portion of this standing wave is sampled by scattering nanodots regularly positioned along the waveguide; the nanodots are characterized by an optical index difference between them and the medium in which the evanescent field is located. For each nanodot, this scattered light is detected by a pixel aligned with this nanodot. The intensity detected is thus proportional to the intensity inside the waveguide at the exact location of the nanodot. A mathematical function known as a Lippmann transform—which is similar to a Fourier transform—takes into account all the calibration data and, when applied to the linear image, produces the spectrum of the light.

The good news for the SWIFTS principle is that the available technologies offer dimensions that provide the spectrometer configuration with very powerful instrumental characteristics. The first SWIFTS proof of concept produced in 2006 was based on a silicon-on-insulator (SOI) waveguide within a CMOS-compatible manufacturing process.¹ The technology is now being developed by Resolution Spectra Systems on the basis of waveguides processed inside quartz wafers.² The nanodots are processed on the surface of the quartz wafer. "Optical" die are sawed and bonded to an assembled CCD or CMOS detector. This hybridization of technologies is an efficient approach in terms of cost, robustness, and reliability (see Fig. 2).

FIGURE 2. A SWIFTS chip is shown; on its left, a ferrule connects the entrance fiber to an optical die bonded to an imaging CMOS sensor. The chip is illuminated by a red laser to better see the waveguide.

Between grating spectrometers and FTS

In terms of functionalities, there are different ways to consider or use this interferometric principle. The measured rough data are in the Fourier domain and result from a linear optical path difference (OPD). At the fixed mirror, the OPD and time difference are zero; this is where the low Fourier frequencies (that is, the energy of the smooth spectral patterns) are located. The farther from the mirror the detected fringes are, the more they correspond to high OPD, high time difference, high Fourier frequencies, and sharper spectral patterns.

The SWIFTS chip can thus be used as an interferometer or a spectrometer. As an interferometer, the chip can measure OPD or optical coherence tomography (OCT) signals directly in the spatial domain or read time correlation. As a spectrometer, the chip can characterize optical signals when applying a Fourier-like function on the rough data or select Fourier frequencies, used for example to detect specific Fourier signatures.

SWIFTS can be considered as a condensed and static evolution of the Michelson spectrometer configuration where the moving mirror and the detector are both functionally replaced by the nanodetectors (each formed by a nanodot and a pixel).

The regular pattern of nanodots can evoke a grating spectrometer. And indeed, SWIFTS can be also considered as an optimization of the grating spectrometer configuration. As explained in Figure 1, a grating spectrometer is in fact also an interferometric system that creates an OPD between both sides of the grating. We demonstrate that for a given resolving power (even when very high), SWIFTS corresponds to the smallest grating configuration that can be found. SWIFTS is not an exotic object but an optimum of spectroscopic configurations and a new category of spectrometer avoiding classical trade-offs in spectroscopy.

Combining resolution, wide range, and speed

The design and performance of a SWIFTS spectrometer are driven primarily by the CCD or CMOS detectors' pixel pitch and format. Typically, a SWIFTS chip 30 mm long, corresponding to a linear detector with 2000 15 μm pixels, will provide an ultra-high spectral resolution of 70,000; that is, 0.005 nm at 630 nm, which can be alternately stated as 0.2 cm^-1 or 6 GHz. The same hardware can be typically calibrated and used over a spectral range of about 400 nm. The overall system's signal-to-noise ratio (SNR) can theoretically reach 30 to 50 dB, depending on the configuration.

The first of two limitations of the basic configuration illustrated in Figure 1 is that the throughput is that of a single-mode waveguide, which has an optical étendue equal to the square of the wavelength. Second, the nanodetector pitch of a few microns results in a simultaneous band capability of about 5 to 15 nm in the visible/near-IR spectrum, which could be too narrow for some applications.

However, both of these limitations can be overcome by a multiplex configuration consisting of N shifted parallel waveguides coupled to a multimode fiber, which multiplies both the optical étendue and the bandwidth by N (with N typically around 50 to 100). This multiplex configuration is, for instance, able to measure in one integration time a spectral range wider than 4000 cm^-1with no limitation on the spectral resolution and a throughput equivalent to a spectrometer fed by a 200-μm-core multimode fiber through a slit. Furthermore, the multiplex (otherwise known as Fellgett's) advantage provides a relative improvement in the SNR; with respect to an equivalent dispersive system, this improvement is approximately equal to the square root of the number of sample points comprising the spectrum. As a result, typical configurations are able to detect signals at the nanowatt scale inside the entrance fiber.

In contrast to scanning systems such as optical spectrum analyzers, the speed of one measurement does not depend either on the resolution or on the spectral-range width. Because there are no moving parts, measurement speed is only limited by the sensitivity and the detector frequency.

The absence of moving parts, the high level of integration, and the linear geometry of the technology guarantee highly robust wavelength calibration that can last for a significant period of time and can withstand frequent temperature fluctuations as well as frequent transportation. Because temperature calibration is taken into account during data processing as a linear thermal-expansion factor, temperature fluctuations during measurement do not reduce the absolute accuracy. For example, several SWIFTS instruments have traveled many thousands of miles worldwide without losing their picometer absolute accuracy.

Laser characterization and Bragg sensing

One obvious application of SWIFTS is the characterization of laser sources, possibly at high rates and without temporal artifacts, a need that is not covered by any other technology.³ A simple ultracompact system can provide the functions of a multiwavelength meter, laser tuning control, laser-diode operating point search, spectral mapping, and complex source analysis.

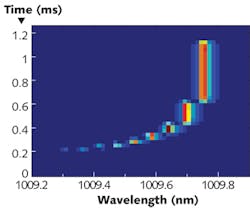
The SWIFTS principle has been implemented by Resolution Spectra Systems in the ZOOM Spectra, an ultra-high-resolution high-rate (up to 30,000 frames per second) spectrometer/multiwavelength meter (see Fig. 3).

FIGURE 3. A VECSEL source undergoes a fast start at wavelengths around 1010 nm; the high-rate capability of the ZOOM Spectra SWIFTS-based spectrometer allows observation of this phenomenon, which lasts less than 1 ms over a 0.5 nm spectral range.

This instrument is particularly valuable for light sources such as distributed-feedback (DFB) lasers, vertical-cavity surface-emitting lasers (VCSELs), external-cavity laser diodes, OPOs, and others, for characterization that current laser spectrum analyzers (LSAs), optical spectrum analyzers, wavelength meters or other spectrometers cannot correctly perform. Characterizations include measuring very unstable laser sources; finely characterizing a multimode laser by discriminating all modes and measuring their absolute wavelengths; performing many measurements to characterize a laser in a reasonable time; performing wavelength tuning on a laser at high speed; monitoring a tunable laser and checking in detail what happens as it mode-hops; and integrating a LSA /wavelength-meter function into a laser.

The technology is also currently being used for interrogation of fiber Bragg-grating sensors, allowing multiplexing of many channels with a small, robust unit. The resulting 40 × 40 × 10 mm spectrometer component is particularly attractive for embedded applications. As an illustration, the ZOOM Spectra has been recently used to collect a large quantity of Fourier spectra in order to statistically detect earthquakes at a distance of more than 10,000 km from the epicenter of the quake.

Mainstream applications

The principle of the Michelson Fourier-transform spectrometer was known for a long time before such spectrometers became available as a commercial product, aided by the advent of fast computers. In a similar fashion, Lippmann's 1908 century-old methods can now be implemented as SWIFTS, thanks to nanotechnology; we can reasonably expect that this technology will address several key applications in the near future.

Raman spectroscopy is probably one of the most interesting sets of applications to be addressed with SWIFTS. The market-fit issue mentioned previously is especially significant in this domain: laboratory systems offer 0.2 to 5 cm^-1 resolution while mini-Raman systems achieve 10 to 30 cm^-1 resolution with very poor absolute accuracy, resulting in a lack of solutions for applications needing high performances in a nonlaboratory environment. This is exactly the area where the SWIFTS matrix configuration can play a key role.

References

1. E. le Coarer et al., Nat. Photon., 1, 8, 473–478 (2007).

2. C. Bonneville et al., "SWIFTS: A groundbreaking integrated technology for high-performance spectroscopy and optical sensors," Proc. SPIE 8616, 86160M (2013).

3. F. Thomas et al., "High-performance high-speed spectrum analysis of laser sources with SWIFTS technology," Proc. SPIE 8992, 89920I (2014).

Christophe Bonneville is cofounder and president of Resolution Spectra Systems, Meylan, France; www.resolutionspectra.com; email: [email protected].