OPTICAL COHERENCE TOMOGRAPHY/TISSUE PHANTOMS: A physical eye model for OCT

T. SCOTT ROWE

In the field of ophthalmology, standard, well-characterized "test eyes" (tissue phantoms) are generally available to enable development and comparison of diagnostic instruments. The corneal topographer, the refractometer, and, more recently, the wavefront aberrometer all have the benefit of readily available test eyes designed to help evaluate their application performance. The need for a standard test eye is now becoming apparent as well for ophthalmic optical coherence tomography (OCT) instruments. Such a model would have many uses, including:

a) A target for demonstrating OCT functionality and imagery. A standard model or "eye" allows for instruments to be compared and features demonstrated, for instance, at trade shows.

b) A target for training OCT operators, technicians, and repair personnel, freeing up others from having to serve as a target while the technician learns. Studies show that well-trained ophthalmic technicians produce consistent measurements.

c) A target for OCT researchers and engineers, allowing for the development and calibration of automatic layer segmentation software with known retinal layer dimensions. Eye safety issues are not a concern with an eye model/tissue phantom.

d) A target for evaluating clinical systems from multiple manufacturers for clinical trial purposes. It has been well documented^4,7,8,10 that clinical systems from different manufacturers—particularly time domain vs. spectral domain—do not match in terms of RT measurements. A "standard" model eye that is easily shipped could be used to correlate instruments of differing technologies and manufacturers.

Clearly defined criteria

For the development of tissue phantoms in general—and eye model tissue phantoms in particular—it is helpful to be clear regarding purpose. The more detailed and precise the definition for use, the better the chance of success: General eye models and phantoms rarely meet any serious commercial or research requirements.

In developing a novel test eye¹¹ for ophthalmic OCT, we determined that a tissue phantom of a normal human retina would need to be sufficiently detailed to allow for unambiguous imaging, and replicate the architecture and morphology of the fovea, with sufficient layer definition to allow for automatic layer segmentation by the instruments—thus allowing for retinal thickness (RT) measurements, an important clinical measurement. Initially, the field of view could be limited to 18° (<5 mm in diameter), but the phantom would have to be embedded in an eye model that would enable the rapid alignment and acquisition of the phantom. The eye model should also be constructed such that it would not require fluids that need to be cleaned or maintained: ideally, it would be a solid-state construction.

Tissue optics and phantom design

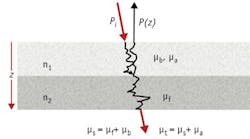
Building a tissue phantom for OCT with proper optical properties necessitates consideration of how the OCT signal is generated. The following equation describes in one dimension the intensity of backscattered light as it propagates through tissue:^{5, 6}

where Γ is a function depending on source coherence, P_i is the incident beam intensity at the tissue, R is the Fresnel reflection from a tissue interface, μ_b is the backscatter cross-section coefficient, μ_t is the total attenuation scattering coefficient, and μ_t = μ_a + μ_s, δ(z-z_n) is a delta function (depicting location of reflecting and scattering layers).

The two key elements for phantoms are the backscatter coefficient and the interface reflection. They work together to define the power of backscattered light that the OCT collects and, in order to achieve a realistic intensity, the signal return from the phantom depends on this combination of backscatter and reflection being equivalent to the modeled tissue. A key point to make here on the Fresnel reflection is that at any tissue interface involving different indices of refraction n₁ and n₂, R = (|n₁ - n₂|/(n₁ + n²))² at normal incidence. Thus, it is possible to construct phantom interfaces using optical materials with absolute indices different to those being mimicked, as long as their adjusted Rs are close (see Fig. 1). Accommodation will need to be made for the differences in optical path lengths (thicknesses) in the design, but this opens up a much wider range of materials than what is normally discussed for tissue phantoms.

A major goal in designing this retinal phantom is to achieve good backscattering properties for each layer from an OCT perspective. We assigned the following morphology:

a) A total retinal thickness (RT) of ~300 μm. This would put it in the range of normal eyes measured from the inner limiting membrane (ILM) to the top of the retinal pigment epithelium (RPE).^7,8

b) A foveal pit of ~120 μm deep, and a maximum diameter of 1.2 mm³. This would leave a central retinal thickness of ~180 μm deep, again within the range of normals.^9,10

c) An RT comprised of five layers of 60 μm each. Although not exactly corresponding with all of the neurosensory retinal layers, it comes close, and each layer in this stack can be adjusted for either reflectivity (R) or backscatter (μ_b).

d) An RPE with relatively high R and μ_b, typically 60–80 μm thick. Later designs attempt to separate the inner segments/outer segments (IS/OS) from the RPE with a separate layer.

In a high-resolution OCT cross-sectional image of a normal human retina, many layers are clearly visible (see Fig. 2). The design layout for the retinal phantom mimics this layering (see Fig. 3). A particular challenge was to represent the foveal pit morphology; another goal was to match phantom relative layer brightness and contrast with clinical images so that the automatic layer segmentation software provided with several OCT systems could be tested.

Current revision and future directions

ACKNOWLEDGEMENTS

The author would like to thank Dr. Robert Zawadzki of the UC Davis Department of Ophthalmology and Vision Science for his many helpful suggestions and test images during the development of this eye model and tissue phantom.

References

1. R. J. Zawadzki, T. S. Rowe, A. R. Fuller, B. Hamann, and J. S. Werner, "Toward building an anatomically correct solid eye model with volumetric representation of retinal morphology," Proc. SPIE, 7550, 75502F (2010).

2. R. J. Zawadzki, T. S. Rowe, and J. S. Werner, "Progress Report on Building an Anatomically Correct Solid Eye Model with Volumetric Representation of Retinal Morphology," 2010 ISIE Conference, Fort Lauderdale, FL (May 1, 2010).

3. A. M. Dubis, J. T. McAllister, and J. Carroll, Brit. J. Ophthalmol., 93, 1223–1227 (2009).

4. G. Vizzeri et al., Brit. J. Ophthalmol., 93, 775–781 (2009).

5. J. M. Schmitt, IEEE J. Select. Topics Quantum Electron., 5, 4, 1205–1215 (1999).

6. J. M. Schmitt, A. Knüttel, and R. Bonner, Appl. Opt., 32, 6032–6042 (1993).

7. S. Grover, R. K. Murthy, V. S. Brar, and K. V. Chalam, Am. J. Ophthalmol., 148, 266–271 (2009).

8. S. Grover, R. K. Murthy, V. S. Brar, and K. V. Chalam, Invest. Ophthalmol. Vis. Sci., 51, 2644–2647 (May 2010).

9. P. H. Tomlins and R. K. Wang, J. Phys. D: Appl. Phys., 38, 2519–2535 (2005).

10. I. Krebs et al., Invest. Ophthalmol. Vis. Sci., 52, 6925–6933 (August 2011).

11. T. S. Rowe, "Phantom For Rendering Biological Tissue Regions", U.S. Pat. 8,480,230 (2013).

T. Scott Rowe is principal/chief consultant with Rowe Technical Design, Inc.; e-mail: [email protected]; www.rowetechnical.com.