For many optoelectronic professionals, nonlinear optical effects are not an extraordinary means of generating new wavelengths, but rather a barrier to achieving optimum performance in their systems. Surprisingly, the most far-reaching problems occur in the pure glass used in optical networks.
Commonly used step-index single-mode fiber has a core diameter of less than 10 µm. Dielectric waveguiding maintains this same diameter for a single-mode beam through the entire length of the fiber, with a resultant concentration of beam intensity. The extremely low loss of modern optical fiber then allows the otherwise negligible waves generated by nonlinear processes to grow unattenuated through miles of silica.
Because SiO2 is a symmetrical molecule, silica does possess the inversion symmetry that must be absent for second-order nonlinear optical effects such as frequency doubling to take place. The important nonlinear phenomena in simple optical fiber therefore are third-order effects. These effects are stimulated Brillouin scatter (SBS), stimulated Raman scatter (SRS), four-wave mixing, and a variety of phase-modulating effects that produce channel crosstalk.
A low ceiling
Stimulated Brillouin scattering is the most serious nonlinear obstacle in optical networking, placing an upper limit on the power that can be transmitted in a single-mode fiber. The threshold for the onset of SBS can be as low as a few milliwatts for some systems. Once the threshold for SBS is exceeded, a rapidly increasing percentage of the power launched into the fiber is reflected back toward the transmitter.
The stability of diode lasers is especially vulnerable to such back-reflected light, and communication is degraded in a variety of ways—such as decreased signal-to-noise ratio (SNR), and so on. The SBS threshold decreases with increasing wavelength, and also is lower for narrower linewidth sources.
High-speed 1550-nm systems that use continuous-wave (CW) lasers must take particular care to design for SBS. Such systems are found, for example, in cable television networks. Erbium-doped fiber amplifiers (EDFAs), widely used to boost signal strength between longer network nodes, also decrease the SBS threshold, dividing it by a factor equal to the number of EDFAs used in series.
SBS background
In Brillouin scattering, the electric field of a pump wave produces an acoustic wave in the material. For stimulated scattering, this pump wave is the signal itself, when it has exceeded the threshold intensity. The acoustic wave then causes the index of refraction of the material to vary in a periodic manner, similar to a Bragg grating.
FIGURE 1. In the pattern produced in a Fabry-Perot interferometer resulting from stimulated Brillouin scattering, the strong concentric rings on the left are produced in the absence of SBS; the additional rings on the right are produced by the pump beam down-shifted by the characteristic Brillouin frequency of the material. (Adapted from the first observations of SBS by Chiao, Townes, and Stoicheff, Physical Review Letters 12 ,1964)
This grating reflects the pump wave. The scattered light is shifted downward in frequency due to the Doppler effect caused by the movement of the grating (see Fig. 1). This is a somewhat heuristic description of SBS; for a true picture of the process, a quantum-mechanical description is needed.
In this quantum picture, the pump photon is annihilated, creating a Stokes photon and an acoustic phonon. The angular dependence of the scattering is greatest in the reverse direction, and is zero going forward. The cladding of the optical fiber blocks scattering in other directions.
The Brillouin frequency shift is calculated from
ƒB = 2nvs / λp
where vs is the speed of sound in the material, n is the index of refraction, and λp is the wavelength of the pump beam. Values typical for silica are vs about 6 km/s, and n about 1.45 near 1.5 µm, so ƒB is roughly about 11 GHz.
Threshold values for SBS for systems operating at 1550 nm are often below 10 mW, and can be as low as 1 mW for very narrow linewidth laser sources. Common methods of controlling SBS rely on broadening the spectral width of the signal source without significantly degrading the signal itself. Practical implementations of SBS suppression can raise the threshold by a factor between 2 and 10.
SRS on the rise
Stimulated Raman scattering (SRS) is used to produce broadband amplifiers and tunable lasers using simple silica fiber as the gain medium (see Laser Focus World, October 2003, p. 82). In optical networking, SRS poses a limitation on the performance of wavelength-division multiplexing (WDM) systems by arbitrarily transferring power from one signal channel to another.
Recall that the Raman effect describes the production of a new wave, also called the Stokes wave, by the inelastic scattering of a pump beam by optical frequency phonons, in this case in silica fiber. The energy of the new Stokes wave is determined by the characteristic phonon energy of the material. In silica, this frequency shift is about 13 THz.
Because of the high level of pump power required, SRS is a less serious problem for optical networking than is SBS. In practical systems, the SRS threshold is on the order of 1 W, more than two orders of magnitude greater than SBS. However, networks using EDFAs are already using powers near 500 mW, and, as with SBS, amplifiers in series decrease the SRS threshold.
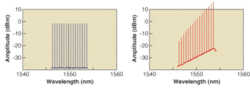
In WDM systems, SRS provides a broad source of gain for longer-wavelength channels, which are pumped by the shorter-wavelength channels. The net result is a reduction in the power in the channels that become pump wavelengths, and an uncontrolled increase in the power in the longer-wavelength channels (see Fig. 2). This is referred to as Raman-induced crosstalk.
FIGURE 2. Stimulated Raman scattering in multichannel systems such WDM results in weakening the shorter-wavelength signals that pump longer-wavelength channels (the figure is for illustration purposes only).
In fact, SRS is the principal source of crosstalk in 1.55-mm systems that use non-dispersion-shifted fiber (NDSF).
One means of dealing with SRS is spectral inversion. If the spectrum of the WDM signal is inverted at some appropriate distance in the transmission line, the longer-wavelength channels become the shorter, and vice versa. Then SRS itself in the remaining fiber length reverses the imbalance it has caused.
Four-wave mixing
Another type of crosstalk that affects certain types of systems results from four-wave mixing, a general type of third-order nonlinear optical phenomenon. Unlike the stimulated scattering discussed above, four-wave mixing does not involve changes to the energy state of the medium, which merely serves a catalytic or "parametric" function in combining incident waves to produce new ones.
Like other nonlinear effects in silica, the coefficients for four-wave mixing (FWM) are very weak. In addition, four-wave mixing requires that all of the waves—old and new—interact over a minimum effective distance in the material, a constraint referred to as phase matching. Nevertheless, four-wave mixing can be a serious concern for systems that carry a large number of closely spaced channels, most notably in WDM.
Consider three closely and equally spaced frequencies ω1, ω2, and ω3 in a WDM system. Four-wave mixing combines these three waves in sum and difference permutations to produce new frequencies:
ω1 + ω2 – ω3, ω1 –ω2 + ω3, etc.
Some of these new frequencies are far outside the transmission band of the WDM system; nine waves fall near enough to the WDM band to be of concern.
Of the nine new waves, three will have frequencies that exactly match one of the original signals, and it will not be possible to filter them out. Even though the majority of the new waves can be filtered, the number of such potentially interfering waves increases rapidly as the number of channels rises. For N signals, the number of potentially interfering waves increases as 1/2 (N3 – N2).
Coping with mixing
This rapidly becomes a very large number—a 40-channel system, for example, in theory could produce more than 30,000 such waves. The only solution is to prevent them from forming. For a given channel spacing, control of four-wave mixing relies on the dispersion characteristics of the fiber.
The efficiency of FWM is inversely proportional to the level of fiber dispersion, and is strongest at the zero-dispersion point. For a standard channel spacing in non-dispersion-shifted fiber, four-wave-mixing efficiency is negligible. If dispersion-shifted fiber (possibly together with a narrower channel spacing) is used, then FWM can be very significant.
So-called NZ-DSF (nonzero dispersion-shifted fiber) was developed to address FWM and other nonlinear concerns. Designing an optical fiber with zero dispersion in the transmission band will maximize its bandwidth, but also maximize the effects of certain nonlinear phenomena like four-wave mixing. NZ-DSF places the zero-dispersion point close to, but outside of, the 1550-nm transmission window.
Other methods of dealing with FWM include spacing the channels at uneven wavelength intervals to reduce the coincidence of FWM products with channel frequencies, and inserting into a network special fiber lengths or devices that have opposing dispersion characteristics that reverse the dispersive effects of the main fiber length.
Modulation
A variety of nonlinear phenomena similar or related to self-phase modulation (SPM) can also give rise to effects like crosstalk. Recall that SPM refers to the change in the phase of an intense pulse as it modifies the index of the refraction of the material that it passes through. Cross-phase modulation and intermodulation occur when the intensity of one channel is sufficient to change the refractive index of its neighbor. In some cases, the only means to control such effects is to increase the diameter of the optical fiber.
Next month's article concludes this series with a survey of some of the more exotic applications of nonlinear optical effects.