Quantum-dot Sources: Quantum dots for future optical quantum technologies

THOMAS MEANY
Quantum dots are low-dimensional structures that permit the isolation of a small number of charges. One example is the confinement of a single electron-and-hole pair, or exciton, which can recombine to produce radiation. In this way, the structure acts very much like an artificial atom, with the emission wavelength of the radiation defined by a specific energy-level transition with a characteristically narrow linewidth.
Quantum dots inherently emit only a single photon at each excitation. The population of the quantum-dot energy levels can be controlled electrically or optically, meaning that the device can be used for on-demand production of photons.1 It is this behavior that has made quantum dots such desirable structures for future optical quantum technologies.
Quantum information is demanding in its requirements. It requires large numbers of quantum bits, or qubits, that can be easily prepared in a specific state exhibiting low decoherence and yet can interact with one another controllably. These qubits may be spin states of atoms, ions, or molecules, or the direction of current flowing in a superconducting loop. The key requirement is that the state of the two-level system can exist in a superposed state where the system is simultaneously in both states rather than in simply one state or another (for example, off or on).
An optical qubit can be formed using any of the degrees of freedom of a photon, including distinct polarizations, temporal modes, spatial modes, or frequencies. These are easy to prepare in a desired state and exhibit low decoherence. The unfortunate catch is that photons do not easily interact with one another, meaning that ingenious methods must be devised to produce nonlinear interactions such as exploiting projective measurement or cavity quantum electrodynamics.
Quantum dots in semiconductors therefore make an excellent source of qubits. Not only are they intrinsically small, but they can also be incorporated into devices such as cavities, photonic crystals, and diodes (see Fig. 1). This permits extremely precise engineering of emission wavelength and confinement in photonic circuits. Quantum dots also offer the potential for deterministic generation—something that another method of photon generation, spontaneous parametric downconversion (SPDC), is inherently incapable of.The fabrication of quantum dots is achieved using a strain-induced formation technique called Stranski-Krastanov growth. This approach uses thin film-deposition techniques such as molecular-beam epitaxy (MBE) or metal-oxide vapor-phase epitaxy (MOVPE). Atomic sheets are grown layer by layer, and when there is a mismatch between the lattice constants of two different layers, strain builds and eventually results in the formation of islands, which then act as quantum dots.
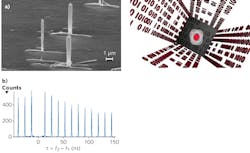
This random nucleation is nonideal and a number of methods are used to accommodate for this inconvenience. In one approach, the randomly nucleated sites are optically assessed in a specially equipped cryostat that enables in situ electron-beam lithographic inclusion of desirable candidate quantum dots into finished devices.2 Alternatively, growth can be forced to occur in a predefined location by pre-patterning the substrate to produce preferential growth locations, meaning that subsequent device processing can occur at these predetermined locations (see Fig. 2a).3 A final approach involves the development of the photonic structure during fabrication, as has been achieved using "pyramidal" quantum dots, which are uniformly embedded in a pyramid-shaped photonics structure to aid coupling into an optical fiber.4Technologies
To date, numerous photonic devices have been engineered that help to position quantum-dot light sources as the leading candidate to form a quantum processor. The first adaptation is the incorporation of a diode structure, thus enabling electrical injection of carriers (see image at the top of this page).5 This literally permits push-button operation, which is essential for integration into future densely populated optical computers. The diodes can also be run in reverse to permit wavelength tuning of the quantum dots through the Stark effect.
Another advance is the generation of not just single photons, but entangled photon pairs from a single quantum dot.6 This is achieved by a pair of excitons—or a biexciton—confined in the quantum-dot potential, which recombine through two indistinguishable paths. The result is a pair of photons in an entangled state of right or left circular polarization.
This approach is extremely practical. For example, the process of quantum teleportation requires an entanglement resource to transfer the state of an input qubit from a sender (Alice) to a receiver (Bob). Such a technique requires that the entanglement resource be shared between Alice and Bob.
In the process, a Bell state measurement is performed on Alice's half of the entangled state and the qubit that she wishes to transmit. Bob's half of the entangled state is projected into the state of Alice's qubit minus a single qubit rotation, which must be fed forward. This single qubit rotation is a classical bit and therefore prevents the superluminal transfer of information between Alice and Bob. Teleportation has been demonstrated using an entangled resource generated from a quantum-dot entangled LED, which can potentially be incorporated into future secure quantum communication systems.7
The use of confining structures has emerged as an essential method for engineering the optical properties of the quantum dots as well as their incorporation into photonic circuits. Light can be confined in a photonic structure not just though refractive index contrasts resulting in total internal reflection, but also through band-gap confinement. The photonic band gap is formed in much the same way as an electronic band gap. A periodic modulation in the refractive index results in forbidden energy bands (see Fig. 2b).
Confinement in one-dimensional cavities such as micropillars has the effect of increasing the probability of emission through Purcell enhancement. This has been used as a source of highly indistinguishable single photons, as well as a method for deterministic nonlinear interaction through cavity quantum electrodynamics.8 Two-dimensional confinement in photonic-crystal waveguides has enabled the on-chip integration of photons generated using quantum dots; waveguide coupling efficiencies of 98% have been demonstrated.9
Outlook and challenges
Unfortunately, quantum dots still have a number of challenges to address before becoming truly practical. The three lingering issues are the requirement for low temperature (<10 K), the need for long-wavelength emission, and achieving high-visibility interference between two quantum-dot photons.
The low-temperature requirement is the least likely to be overcome and in some cases is not hugely significant, as it is still practical to build a large-scale quantum computer with only a linear increase in cooling resources. However, this issue would render a long-distance quantum repeater using multiple distributed entangled LEDs impractically expensive.
Long-wavelength quantum-dot emission has been achieved, but has yet to reach beyond 1.3 μm (the O-band).10 This wavelength already increases the distance over which a quantum communication channel could be maintained, with a 20 dB loss from 7 km at an 850 nm wavelength to 55 km at 1.3 μm. Reaching the C-band (1530-1565 nm) would increase this distance to 100 km. Furthermore, low-cost optimized components for wavelength filtering and routing are available at wavelengths in the O- and C-bands.
The final hurdle that is being addressed is the generation of indistinguishable photons that show high two-photon interference visibilities. This two-photon interference manifests when photons that are indistinguishable in every degree of freedom demonstrate significantly different probability distributions as a result of which-path interference.
This is best illustrated by the 1987 experiment of C. K. Hong, Z. Y. Ou, and Leonard Mandel performed at the University of Rochester (Rochester, NY) in which a pair of indistinguishable photons that pass through a beamsplitter are seen to "coalesce," both appearing in a single output and never in separate outputs. This effect is crucial to optical quantum computing using linear optical elements, as engineering an effective photon-photon interaction is achieved by post-selection on a specific output distribution. The linear optical gate, which imparts a π phase shift on a target mode dependent on the presence of a single photon in a control mode, is a beamsplitter with a 1/3 reflectivity. This gate, a controlled-phase gate, operates probabilistically with a probability of 1/9. However, the operation of this controlled-phase gate is critically dependent on the two-photon interference visibility.
This dependence is something that plagues quantum dots: while they very accurately mimic the behavior of a single atom, they are composed of multiple defects that result in stray charges and other decoherence-inducing phenomena. Few solutions are available, but the most successful has been exciting the transition on resonance thereby exciting no other potentially decohering carriers.11
In the future, it is highly likely that techniques such as substrate patterning prior to quantum-dot growth will result in much higher yields of uniform single-photon-emitting quantum dots. Advances in fabrication and device development will further increase the range of functions available on a single chip. By increasing two-photon interference visibilities and, most importantly, showing that distinct quantum-dot sources can produce highly indistinguishable photons, it will be possible to produce advanced logic-gate operations.
REFERENCES
1. C. Santori et al., Nature, 419, 594 (2002).
2. M. Gschrey et al., Appl. Phys. Lett., 102, 251113 (2013).
3. J. Skiba-Szymanska et al., Nanotechnol., 22, 065302 (2011).
4. G. Juska et al., Nature Photon., 7, 527–531 (2013).
5. Z. Yuan et al., Science, 295, 102 (2001).
6. C. L. Salter et al., Nature, 465, 594 (2010).
7. J. Nilsson et al., Nature Photon., 7, 311–315 (2013).
8. D. Englund, Nature, 450, 857 (2007).
9. M. Arcari et al., Phys. Rev. Lett., 113, 093603 (2014).
10. M. B. Ward et al., Appl. Phys. Lett., 86, 201111 (2005).
11. A. J. Bennet et al., "Cavity-enhanced coherent light scattering from a quantum dot," arXiv:1508.01637 (2015).
Thomas Meany is a researcher at Toshiba's Cambridge Research Laboratory (Cambridge, Cambridgeshire, England); e-mail: [email protected]; www.toshiba.eu/eu/cambridge-research-laboratory.