Neural Networks for Optical Analysis: Deep neural network accurately retrieves phase information from 3D point-spread functions

Most optical imaging techniques capture only intensity information, meaning that phase information on the wavefronts incoming to the sensor is lost. For some types of imaging systems, such as microscopes, where objects may be transparent but affect phase, the detection or retrieval of phase information could help improve the imaging process. Phase retrieval, which is the computational recovery of hidden phase information from intensity information, exists but in its conventional forms is slow, requiring intensive computation to retrieve any useful amount of phase information.

In response to this problem, Leonhard Möckl, Petar Petrov, and W. E. Moerner of Stanford University (Palo Alto, CA) have developed a phase-retrieval technique based on deep residual neural networks (NNs) that quickly and accurately extracts the hidden phase for general point-spread functions (PSFs), returning the information as Zernike coefficients. A deep NN has multiple network layers between the input and output; in this type of NN, data works its way from input to output through the layers without any feedback (looping of data backward).

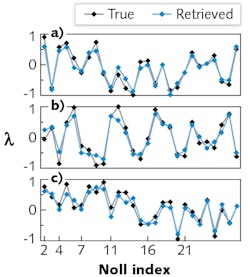
The Stanford phase-retrieval approach is based on a so-called deep residual NN, in which bits of information percolating through the NN sometimes skip layers, which can be an aid to training the NN. After the NN is trained, it uses as input a small set of 2D intensity measurements of a PSF taken at a range of through-focus positions. The NN processes the information and outputs Zernike coefficients of orders 1 through 6 (corresponding to so-called Noll indices of 2 through 28; Noll indices, which are one-dimensional numbers, are simply mapped from Zernike orders, which are two-dimensional, allowing a specific Zernike order to be represented by a single number).

To test the effectiveness of their NN, the Stanford researchers simulated numerous PSFs, each the result of a different randomly chosen set of Zernikes of orders 1 through 6; PSF simulations were calculated for focal positions of -1, -0.5, 0, 0.5, and 1 µm, with variations as high as 2λ in the Zernike coefficients. The resulting PSFs were used as input for the NN.

Neural network training

In training the NN, the researchers determined that a large number of training PSFs were required—200,000 was not enough, and they finally settled on an amount of 2,000,000 PSFs. They considered a number of different types of NNs before settling on the residual NN architecture. Training time took about 12 hours. The resulting trained system could analyze a PSF in 5 ms on a standard desktop PC having an i7–6700 processor, 16 GB RAM, and no graphics processing unit (GPU), although for additional speed the system was implemented on a standard desktop PC with 64 GB RAM, an Intel Xeon E5–1650 processor, and an Nvidia GeForce GTX Titan GPU.

The NN could successfully predict the Zernike coefficients quite accurately for each PSF analyzed (see figure). The researchers also took the output Zernikes, calculated the resulting PSFs, and compared them to the input PSFs, which showed good agreement. In addition, they analyzed a predetermined PSF, called Tetra6 PSF, that is used practically to locate nanoscale emitters in 3D. The NN accurately predicted the Zernike coefficients, including some that were outside of the NN’s training range.

The researchers add that their approach can potentially be expanded to do phase retrieval of non-Zernike-like phase information, and could also be helpful in the design of phase masks.

REFERENCE

1. L. Möckl, P. Petrov, and W. E. Moerner, Appl. Phys. Lett., 115, 251106 (2019); https://doi.org/10.1063/1.5125252.