Tabletop optical alignment: A nightmare for QED scientists (with a solution)

A quantum computing company reached out with a tabletop optical alignment nightmare situation, so we loaned them an autostigmatic microscope to demo. Although they had no experience using our Point Source Microscope, within a week they had achieved their best performance to date.

At first glance, the alignment of tabletop optical elements may seem straightforward: follow the laser beam path with a card and center lenses on the beam. But the alignment requirements are as tight or tighter for more complex systems, such as those used in quantum computing, than for imaging optics. A new method promises to transform this process—by allowing for the alignment of tabletop optics to <1 µm of decenter and <5 microradians of tilt using a Bessel beam as the reference axis.

Why are the requirements tighter? Aberrations to laser beam quality are not linear with numerical aperture (NA) and field of view (FOV), but increase as their square and higher powers. The same goes for aberrations introduced by lens decenters and tilts—their effects increase nonlinearly with misalignment. You can do nothing about the aberrations due to the design, but the design of your system is simulated and optimized with code using perfectly aligned and manufactured optical components. The designed system’s hardware performance won’t achieve the design performance without flawlessly aligning each element in at least five degrees of freedom. This is the nightmare: How do you do it?

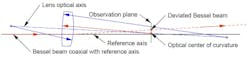
Luckily, you have an option unavailable in many imaging optical systems: Commercial off-the-shelf (COTS) mounts that allow fine adjustment in five degrees of freedom. Theoretically, each lens’s optical axis can be made coaxial with a reference axis, and lens spacings can be adjusted. In addition, you can use a Bessel beam as a reference axis because it propagates through an optical system like a single ray in a lens design program.¹ The Bessel beam and a reflection from the center of curvature of one of the lens’s surfaces provide the two points used for feedback to adjust the lens’s optical axis so it is coaxial with the reference axis.²

Alignment

The alignment process involves an autostigmatic microscope (ASM) or autocollimator with a microscope objective. It is used to view the Bessel beam, illuminate the lens’s spherical surface from its optical center of curvature, and view the reflected image. The lens’s optical axis is coaxial with the reference axis when the two spots are centered on the crosshairs in the ASM pre-aligned to the pinhole light source. Figure 1 shows a lens inserted into a Bessel beam after the ASM was centered on the beam. Neither the Bessel beam nor the optical center of curvature now lie on the axis of the original beam due to the misalignment.

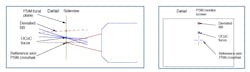
Figure 2a is a detail of the focal plane where the ASM views the two spots, while Figure 2b shows the spots and crosshair as viewed on a monitor or through an eyepiece.

In an easy and quickly converging iterative procedure, the lens is decentered to bring the Bessel beam onto the crosshair. Then, the lens is tilted to bring the optical center of curvature onto the crosshair. This step slightly decenters the Bessel beam, so the lens must be recentered and then tilted. The process usually takes 3 to 4 iterations to bring the alignment to <1 µm and <5 microradians tilt from a condition where both light spots are aligned well enough to enter the microscope objective (see Fig. 3). The figures show the alignment process in two dimensions, but it works for all three dimensions.

Since the Bessel beam used as the reference axis is again coaxial with the initial beam after exiting the aligned lens to small tolerances, the beam is used to align the next lens in the chain. The same procedure is used lens after lens until the system focuses on the target.

Convergence

Convergence is iterative as a practical matter. If the lens could be rotated about the point where the optical axis crosses the reference axis, just to the right of the optical center of curvature in Figure 1, the alignment could be accomplished in one step. Almost all adjustable lens mounts tilt the lens about a pivot close to the lens, and tilt about this point decenters the Bessel beam slightly so further correction is needed. But this is a simple task since the two light spots are continuously visible on the monitor, and the process converges rapidly (see Fig. 4).

Figure 4a shows the simulated, iterative alignment convergence using lens design code to drive the Bessel beam ray height or center of curvature to zero. Figure 4b shows the iterative convergence for an experimental alignment result for a similar but not identical lens used in the simulation. The distance from the reference axis is on a log scale in the graphs because a linear scale would not show the details of how the alignment converges at a typical factor of 3 to 4x each cycle. Also, negative distances were treated as positive. Zero makes no sense on a log scale, but it is intended to represent the ASM's resolution limits.

The figure also shows how the Bessel beam alignment slightly misaligns with the center of curvature alignment in the first half of the alignment cycle, and then tilting the lens misaligns the Bessel beam. Also, the sensitivity of the Bessel beam to tilt is less than the sensitivity of the center of curvature for the positive lens used as an example. And it is helpful to know that for any lens and pivot point, it is possible to simulate the improvement in alignment before doing the alignment in the lab so potential alignment problems are known in advance.

It is clear from Figure 4a that it is possible to go from a substantial misalignment in tilt and decenter to full alignment to the limits of resolution of a suitable detector in 3 to 4 iterative alignment cycles using continuously available data on the degree of misalignment. This means it is possible to align a lens within less than a minute to <1 µm in decenter and <1 second of arc, given a practical radius of curvature used for centering.

Using an autostigmatic microscope, lens mounts with 5 degrees of freedom, and a Bessel beam as a reference axis, it is possible to achieve alignment precision comparable to or better than using a rotary axis as a reference. If the right tools are used, the tabletop optical alignment nightmare for QED researchers is over.

REFERENCES

1. M. Santarsiero, Opt. Commun., 132, 1–2, 1–7 (1996).
2. R. E. Parks and R. Greenberg, Proc. SPIE, 13133, 1313303 (Sep. 2024); https://doi.org/10.1117/12.3027687.