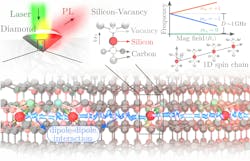
Spin center arrays serve as analog quantum simulators
Quantum simulation is a powerful tool that can realize Hamiltonians—an operator that corresponds to the total energy of the system—that contain impactful physics but may not occur naturally. Analog quantum simulators are physical systems that are relatively easy to control, such that the Hamiltonians realized by the simulators have many tunable parameters that allow for the simulation of a wide variety of models within a wide range of parameter space. Furthermore, these simulators can be experimentally probed to study the models further or even potentially be made into devices that exploit the phenomena that arises within the models for practical purposes.
Due to the exponentially increasing degrees of freedom with respect to the size of quantum systems, quantum simulators are better suited to study many aspects of quantum systems than classical computers. We and our collaborators propose a solid-state analog quantum simulator for the study of critical floating phases and commensurate to incommensurate phase transitions.1
Solid-state quantum simulator
Our proposed quantum simulator is a one-dimensional chain of anisotropic S=1 spin centers that interact through the magnetic dipole-dipole interaction and are implanted into a crystal.
Spin centers are defects that can be placed in a crystal and due to their unique electronic properties, they behave as localized spins. They can be initialized and read out by lasers, and are well known for having long coherence times that persist even at room temperature.
While NVˉ spin centers have been widely studied as sensors and high-temperature qubits, the dipolar interaction is relatively weak, so we propose spin center candidates without hyperfine splittings, such as the silicon vacancy center (SiV⁰) in diamond or divacancies in silicon carbide (SiC). Unwanted hyperfine interactions between spin centers and nuclei within the crystal can also be avoided by using isotopically pure crystals where the atoms have zero nuclear spin. Isotopically pure diamond and SiC can feasibly be grown with ¹²C and ²⁸Si for this purpose.
We were initially interested in using S=1 spin centers to simulate lattice gauge theories that are of interest in high-energy physics, but we encountered a roadblock because the dipolar coupling is dominated by the spin centers’ anisotropic Hamiltonian term. However, we quickly found that a new avenue had opened where an external magnetic field can be applied to make the spin centers have a two-fold nearly degenerate ground state, causing them to behave as S=1/2 particles on the energy scale of the dipolar interaction. This makes it possible to simulate a variety of S=1/2 phases and critical behaviors with spin centers. Notably, this includes floating phases, which in this case are incommensurate spin density waves, and quantum phase transitions such as a line of transverse-field Ising transitions and Berezinskii-Kosterlitz-Thouless and Pokrovsky-Talapov points. These phases and transitions can be controlled via external magnetic fields and varying the orientation of the spin center chain within the crystal.
While there has been interest in quantum simulating floating phases and commensurate-incommensurate transitions, and there have been proposals and experiments to do so via ultracold atom quantum simulators, such as Rydberg atom arrays, this is the first proposal to realize these behaviors in a solid-state quantum simulator.
With current techniques, this quantum simulator is difficult to experimentally achieve. It requires spin centers to be precisely implanted, with even spacing at about 5 to 10 nm. This maximizes the dipolar interaction while the spin exchange interaction remains negligible. While some groups are closing in on being able to implant spin centers with near 10-nm separations, it will require more work to build a chain long enough and evenly spaced enough to realize the physics that we expect from this system.
It is worth noting, however, that spin-center-based qubits are a leading candidate for room- temperature quantum computing, and improving upon techniques to precisely implant nearby spin centers is necessary for this milestone. Another complication is that due to the weak nature of the dipolar coupling between spin centers, this simulator is expected to operate at temperatures near and below 10 μK. This low temperature regime is currently unreachable in experimental settings. Furthermore, it is difficult to initialize and read out information from spin centers placed so closely together.
While these experimental challenges limit the utility of this quantum simulator in the present, we are able to address these challenges for future spin-center-based quantum simulators by considering stronger and longer-ranged interactions between spin centers. There are promising proposals to engineer spin-spin interactions between spin centers with these qualities by using bosonic modes as mediators.2, 3 Moreover, it is predicted spin centers will still have very long coherence times even after introducing bosonic modes to the system.
Considering different interactions between spin centers and more complicated geometries of spin center arrays than a straight one-dimensional chain will provide a lot of versatility for Hamiltonians that can be simulated. For example, higher-dimensional arrays of spin centers could be a promising platform for the study of spin dynamics such as spintronics, which takes advantage of spin degrees of freedom to store and transfer information remarkably efficiently, and topological solitons, which are of high interest across many fields of physics.
As we have shown, there is great potential for spin-center-based quantum simulators to simulate impactful physics and have avenues available to address experimental limitations. We believe there is a promising future for spin-center-based quantum simulators.
REFERENCES
1. T. Losey et al., Phys. Rev. B, 110, 014413 (2024).
2. D. R. Candido, G. D. Fuchs, E. Johnston-Halperin, and M. E. Flatté, Mater. Quantum. Technol., 1, 011001 (2021).
3. M. Fukami, D. R. Candido, D. D. Awschalom, and M. E. Flatté, PRX Quantum, 2, 040314 (2021).
About the Author
Troy Losey
Troy Losey is a graduate student working with Shan-Wen Tsai, a professor of physics and astronomy at the University of California Riverside.
Shan-Wen Tsai
Shan-Wen Tsai is a professor of physics and astronomy at the University of California Riverside.