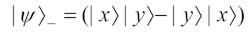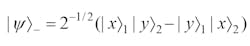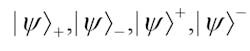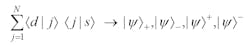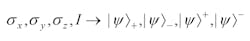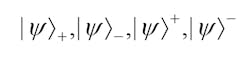The popular press and the specialized literature often exalt the “strangeness” and “weirdness” of quantum mechanics. Certainly, quantum entanglement is the source of such pervasive and engrained opinions. That literature may be forgiven since it follows the philosophical path toward quantum entanglement as initiated by Einstein et al. (EPR),1 and Schrödinger,2 in 1935.
EPR’s opinion toward quantum mechanics as an “incomplete theory” was a powerful statement that promoted hidden variable theories (HVTs).3-5 In the 1950s, Bohm linked the philosophical discussion with knowledge of γ-ray quantum entanglement experiments6 and introduced the concept of an EPR paradox.3, 4
The EPR paradox and HVTs became central to the philosophical path and resulted in the introduction of Bell’s theorem,7 which reinforced von Neumann’s opinion8 classifying HTVs as incompatible with quantum mechanics.7, 8 In turn, Bell’s theorem stimulated the early experiments on quantum entanglement, in the visible optical regime9 that provided the necessary evidence to convince a large portion of the physics community that HTVs were indeed incompatible with quantum mechanics.†
The philosophical path can be summarized as EPR → Bohm and Aharonov → Bell.
The physical path to quantum entanglement began with Dirac’s pair theory10 in 1930 and was reinforced via a 1946 statement from Wheeler, relevant to a hypothetical e+e- → γ1γ2 experiment, which provided the very first definition of what quantum entanglement is: “According to the pair theory, if one of these photons is linearly polarized in one plane, then the photon that goes off in the opposite direction with equal momentum is linearly polarized in the perpendicular plane.”11 This is the essence of quantum entanglement.
Pryce and Ward in 1947 provided the first diagram of a quantum entanglement experiment.12 They also derived the quantum mechanical cross-sections to determine the scattering coincidence ratio caused by a quanta pair, with orthogonal polarizations (| x ⟩ and | y ⟩), propagating in opposite directions.12 The cross-section equation was a function of the now iconic angular term cos 2 (φ1 – φ2) so ubiquitous in quantum entanglement probability calculations. The prediction of Pryce and Ward was soon confirmed13 and scattering experiments powered by γ-ray quanta pairs followed in 1948-1950.6, 14, 15
Bohm and Aharonov5 argued for the γ-ray experiments to be considered applicable to the EPR paradox situation. However, contemporaneous researchers opined that those experiments, even though in agreement with quantum mechanics, did not exclude HTVs.
In retrospect, that opinion was misguided†: “the two photons are entangled, and according to local realism, their polarizations planes should become independent… a typical EPR situation. Already in 1948, observations agreed with quantum mechanics… not with local realism.”16
Here, it is important to emphasize that the physical path of Dirac → Wheeler → Pryce and Ward, which led to the γ-ray experiments, was developed in a complete vacuum from the philosophical path.
The essence of quantum entanglement is its probability amplitude expressed in Dirac’s notation:12,17
that, following normalization, becomes:
Indeed, Pryce and Ward used this equation in their derivation of the correct quantum scattering cross-section disclosed in their 1947 paper. Ward went on to provide a semi-heuristic derivation, using conservation arguments, of this iconic probability amplitude in his doctoral thesis.17
In 1965, Feynman introduced elements applicable to its derivation from a fairly abstract Hamiltonian perspective.18 The Diracian probability amplitude of quantum entanglement was absent from the literature of the philosophical path but appeared out of the blue, without mention of its origin, in the early 1990s.
Depending on the sign and combination of polarization states, for a quanta pair and two channels of propagation, there are four probability amplitudes, or states:
The four states for quantum entanglement can be derived in a transparent mathematical approach using the interferometric Dirac-Feynman superposition probability amplitude,18, 19 so that:20-22
It can be shown that Pauli matrices can also be used to derive the four states of quantum entanglement:22, 23
Since the equations of quantum mechanics are reversible, the probability amplitudes of quantum entanglement can be used to derive both the Dirac-Feynman interferometric principle and the Pauli matrices.22
It is important to emphasize that the N-slit interferometric derivation20-22 of:
is completely free of paradoxes, independent of EPR arguments, and independent of Bell’s theorem.22
Going back to the EPR paper: their crucial premise is an exact measurement of momentum p that leads to an “all values” spread in Δx. This is what led EPR to conclude that quantum mechanics was an “incomplete theory.”1 However, “an absolutely exact measurement of momentum p with Δp = 0 is physically impossible.”21 There is always a non-zero Δp. Once this is accepted, Heisenberg’s uncertainty principle Δx Δp ≈ h applies and the “all values” is no longer a concern.21
Central to the indeterminism of quantum mechanics is the experimentally well-proven nonlocality of the photon.22 Indeterminism, as advocated by Born,24 is crucial to quantum concepts. While discussing quantum mechanics, Feynman stated:18 “Already in classical mechanics there was indeterminability.”
† HTVs, as proposed by Bohm,4 are not quantum mechanical since they cease to obey Born’s rule and sought to overcome Δx Δp ≈ h.22
REFERENCES
1. A. Einstein et al., Phys. Rev., 47, 777–780 (1935).
2. E. Schrödinger, Math. Proc. Camb. Phil. Soc., 31, 555–563 (1935).
3. D. Bohm, Quantum Theory (Prentice-Hall, Englewood Cliffs, 1951).
4. D. Bohm, Phys. Rev., 85, 166–179 (1952).
5. D. Bohm and Y. Aharonov, Phys. Rev., 108, 1070–1076 (1957).
6. C. S. Wu and I. Shaknov, Phys. Rev., 77, 136 (1950).
7. J. S. Bell, Physics, 1, 195–200 (1964).
8. J. von Neumann, Mathematische Grundlagen der Quanten-Mechanik (Springer, Berlin, 1932).
9. A. Aspect et al., Phys. Rev. Lett., 47, 460–463 (1981).
10. P. A. M. Dirac, Math. Proc. Camb. Phil. Soc., 2, 361–375 (1930).
11. J. A. Wheeler, Ann. New York Acad. Sci., 48, 219–238 (1946).
12. M. L. H. Pryce and J. C. Ward, Nature, 160, 435 (1947).
13. H. S. Snyder et al., Phys. Rev., 73, 440–448 (1948).
14. R. C. Hanna, Nature, 162, 332 (1948).
15. E. Bleuler and H. L. Bradt, Phys. Rev., 73, 1398 (1948).
16. R. H. Dalitz and F. J. Duarte, Physics Today, 53, 99 (2000).
17. J. C. Ward, Some Properties of the Elementary Particles (Oxford University, Oxford, 1949).
18. R. P. Feynman, The Feynman Lectures on Physics (Addison-Wesley, Reading, 1965).
19. P. A. M. Dirac, The Principles of Quantum Mechanics, 4th edition (Oxford University, Oxford, 1958).
20. F. J. Duarte, J. Mod. Opt., 60, 1585–1587 (2013).
21. F. J. Duarte, Quantum Optics for Engineers (CRC, Boca Raton, 2014).
22. F. J. Duarte, Fundamentals of Quantum Entanglement, 2nd edition (Institute of Physics, Bristol, 2022).
23. F. J. Duarte et al., Opt. Quantum Electron., 52, 106 (2020).
24. M. Born, Natural Philosophy of Cause and Chance (Clarendon, Oxford, 1949).
About the Author
F. J. Duarte
Research Physicist, Interferometric Optics
F. J. Duarte is a research physicist at Interferometric Optics (Jonesborough, TN), an Optica Fellow (1993), and a Fellow of the Australian Institute of Physics (1987).