LASER COOLING: Cooling of Cr atoms by adiabatic demagnetization is loss-free

Laser cooling of atomic and molecular gases has helped scientists explore the boundaries of low-temperature physics—for example, by creating Bose-Einstein condensates (whose uses include the slowing and stopping of light). But minimizing the loss of atoms or molecules from the trap holding them to be cooled is a major issue. By tolerating some particle loss, laser cooling and trapping followed by evaporation has become the standard technique, though loss-free cooling would be highly welcome.

A method of optical cooling was first proposed in 1950.¹ The technique, which has not been exploited so far, consists of preparing an ensemble of paramagnetic atoms in an external magnetic field in the lowest Zeeman sublevel by optical pumping, waiting for collision-induced thermal repopulation of the higher sublevels (which proceeds at the expense of kinetic energy of the atoms), then optically pumping the atoms back into the lowest Zeeman sublevel, thus cooling the spin system because the emitted photons show higher energy than those absorbed. After the single-cycle temperature reduction, the next cycle can be started at a lower magnetic-field strength, and hence lower Zeeman splitting. Those cycles are expected to proceed without loss of particles. Until recently, however, no papers other than a theoretical work had been published.²

Now, a research group at Universität Stuttgart has applied this technique to 52Cr (chromium) atoms, which are characterized by their high magnetic moment (6µB) in the electronic ground state.³ This high magnetic moment turns out to be highly favorable for the transfer of kinetic energy to the spin system because magnetic dipole-dipole interactions govern the collision process.

Because Cr is often used in semiconductor technology as a mask material, Bose-Einstein condensates—which might enable coherent beams of Cr atoms—could even be of practical technological importance. In addition, once this method is shown to work efficiently it might be applied to many other dipolar atoms and molecules for research in physics.

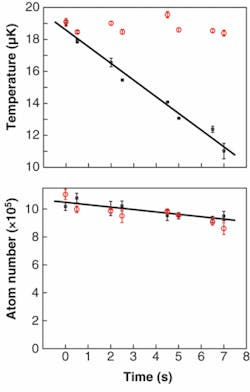
To study the Zeeman cooling cycle, the researchers started with approximately 106 Cr atoms at a temperature of 19 µK in an optical dipole trap of harmonic potential and a depth of 200 µK, established at the beam waist of a 20 W fiber-laser beam at 1064 nm that stores the atoms irrespective of the Zeeman sublevel; they then superposed a homogeneous magnetic field of 1 G. The atoms were aligned in the relevant Zeeman sublevel (mJ = -3) by optical pumping with s-polarized laser light at 427 nm.

Switching the magnetic field from 1 G to 50 mG resulted in a kinetic temperature decrease, measured using absorption imaging and time-of-flight techniques, from 19 µK to 16.5 µK within a 5 s relaxation time. No cooling-induced particle loss was observed. In a continuous cooling sequence, the magnetic field was linearly decreased from 250 mG to 50 mG within 7 s (see figure). The temperature decreased from 19 µK to 11 µK. Again, no cooling-induced particle loss was observed; however, the temperature reached was still a factor of 10 higher than that set by the optical recoil limit (about 1 µK). On the other hand, the authors calculated the demagnetization-cooling efficiency (the gain in phase space density over the loss in atom number) to be 11, which compares favorably to the best value of 4 obtained for evaporation cooling. They conclude that they reached a tenfold higher phase space density for the same number of atoms, a favorable starting point for further evaporation cooling. The atom density reached 10¹³ cm^-3.

By eliminating experimental imperfections, the researchers expect to reach lower temperatures, and possibly the critical temperature for a Bose-Einstein condensate. Furthermore, they see a variety of candidate materials suitable for this cooling process, including rare-earth elements and electrically polar and polarizable molecules.

REFERENCES

1. A. Kastler, J. Physique, Radium 11, 255 (1950).

2. G. Ferrari, Eur. Phys. J. D 13, 67 (2001).

3. M. Fattori et al., Nature Physics 2, 765 (2006).