NONLINEAR OPTICS: Phase-matching in two dimensions achieved with hex-poled lithium niobate
Researchers at the University of Southampton (Southampton, England) have extended linear quasi-phase-matching with periodically poled lithium niobate into a second dimension and will describe their work in an invited paper this month at the Conference on Lasers and Electro-Optics (CLEO) in San Francisco, CA.
Neil Broderick, Graham Ross, and other researchers under the direction of David Richardson have fabricated what they believe to be the first example of a two-dimensional, nonlinear periodic crystal. The refractive index remains constant in the material while the second-order nonlinear susceptibility varies with a spatial periodicity based on hexagonal symmetry in lithium niobate. The theoretical basis for going to two dimensions had been published previously, Richardson said.1 His group simply focused on building a practical model. "We decided we'd work at providing the first demonstration that two-dimensional poling was indeed possible," he said.
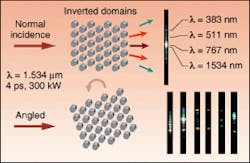
The two-dimensional nonlinear periodic crystal was formed using photolithography to etch a hexagonal pattern into a wafer of lithium niobate (see top image). The hexagonal pattern was aligned to coincide with the natural domain wall orientation of the crystal, and each hexagon comprised a region of domain-inverted material.
The researchers also demonstrated that it is possible to use the additional degree of freedom to simultaneously phase-match more than one nonlinear interaction. To accomplish this, the system was mounted on a platform that provided ±15° of rotation and illuminated with 4-ps, 300-kW pulses at 1531 nm from a high-power, all-fiber chirped-pulse-amplification (CPA) system operating at 20 kHz (see bottom image). The CPA output was focused onto the crystal in 150-µm-diameter focal spot with a peak intensity of about 1.8 GW/cm2 through a 10-cm-focal-length lens.
"We basically demonstrated that it was possible to get multiple phase-matching simultaneously and to get efficient nonlinear parametric processes going at the same time," Richardson said. "We were then able to verify the earlier predictions in terms of the angular dependence of these nonlinear processes. We were able to identify which particular lattice vectors were involved in the nonlinear process through a variety of angle-tuning experiments. And finally, we were able to prove that it was possible to get good efficiencies through this process. So we've got second-harmonic conversion efficiencies up to 50% external [and] up to about 80% internal."
The researchers' primary interests are in making monolithic optical parametric oscillators and in using the additional degree of freedom for switching applications. "It's the first demonstration of extending a very successful technique that has been applied in one dimension for laser resonators, improved frequency conversion, and a whole range of nonlinear processes, to two dimensions," Richardson said.
REFERENCE
- V. Berger, Phys. Rev. Lett. 81, 4136 (1998).
Hassaun A. Jones-Bey | Senior Editor and Freelance Writer
Hassaun A. Jones-Bey was a senior editor and then freelance writer for Laser Focus World.